 ¿Recordáis aquellos años en los que las clases de matemáticas se transformaban en un sinfín de actividades para aprenderse las tablas de multiplicar? ¡Qué momentos!
¿Recordáis aquellos años en los que las clases de matemáticas se transformaban en un sinfín de actividades para aprenderse las tablas de multiplicar? ¡Qué momentos!No sé... tal vez, es tan sólo una impresión personal, pero creo que a la edad de siete o ocho años, una de las cosas más importantes que aprendes son las tablas de multiplicar. Porque esos números alineados y agrupados que simbolizan la compresión de la suma son mucho más que números. Tienen más representaciones y simbolismos. Uno de ellos, es el de que ya eres "mayor". La gente te pregunta ¿Ya sabes multiplicar? Y todo orgulloso o orgullosa respondes, sí, me sé hasta la tabla del... y añades el 6, el 7 o el número de la tabla que estés estudiando en ese momento. Esa sensación de estar descubriendo el mundo y de entrar en los conceptos difíciles, vuelve cuando aprendes a dividir por dos cifras o cuando despejas la primera incógnita de tus ecuaciones. Pero poco a poco, parece que se va difuminando y va perdiendo intensidad...
No negaré, que la Transformada de Fourier estudiada durante mis años universitarios (una aplicación que hace corresponder a una función f con valores complejos y definida en la recta, otra función g definida de la manera siguiente:
No negaré, que la Transformada de Fourier estudiada durante mis años universitarios (una aplicación que hace corresponder a una función f con valores complejos y definida en la recta, otra función g definida de la manera siguiente:
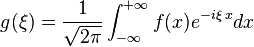 )
)
también me produjo una alegría comparable a la de saber multipilicar... Curiosamente, esta operación matemática está basada en una integral... que no deja de ser la suma de trocitos muy pequeñitos... ¿Tendrán las sumas comprimidas algo especial? ¡Quien lo sabe!
Pero volvamos a las multiplicaciones... ¡A esa primera vez, y a esa tabla del 9! Este fin de semana fui a comer a casa de mis padres, en medio del campo... Y fue entre las montañas, que mi padre me preguntó:
-Irene, a tí te gusta explicar anécdotas de ciencia, matemáticas, tecnología... ¿cómo explicarías tú la tabla del nueve?-
Yo acepté el reto y le comenté... pues diria que multiplicar por nueve es sumar nueve veces el número elegido...
A lo que él me respondió:
-Sí, teoricamente me parece bien... pero ¿Quieres sorprenderte con una regla pnemotécnica que encontré por Internet?!! Mira, extiendo mis dos manos y vamos a contar dedos:
¡Gracias a ellos y a todos los demás porque cuando compartes con alguién tus sueños, el amor se multiplica! ¡Multipliquemos!!
-Irene, a tí te gusta explicar anécdotas de ciencia, matemáticas, tecnología... ¿cómo explicarías tú la tabla del nueve?-
Yo acepté el reto y le comenté... pues diria que multiplicar por nueve es sumar nueve veces el número elegido...
A lo que él me respondió:
-Sí, teoricamente me parece bien... pero ¿Quieres sorprenderte con una regla pnemotécnica que encontré por Internet?!! Mira, extiendo mis dos manos y vamos a contar dedos:
- 9x1=9 Si encojo el dede meñique de mi mano derecha y cuentas los dedos que todavía tengo estirados verás que son exactamente 9
- 9x2=18 Si encojo el dedo anular de mi mano derecha (el siguiente al meñique), verás que me queda un dedo a tu izquierda y ocho a tu derecha, lo que dibuja ¡un 18!
- 9x3=27 Esta vez encogeré el dedo anular y me quedarán el dede meñique y el anular de la mano derecha a tu izquierda y siete dedos más a tu derecha. ¡27!
- 9x4=36 Bajaré el índice de mi mano derecha y obtendré 3 dedos a tu izquierda y 6 a tu derecha. ¡36!
- 9x5=45 Bajaré el pulgar y veremos 4 y5. ¡45!
- 9x6=54 Esta vez, encogeré el pulgar de la mano izquierda y así veremos 4 dedos de mi mano izquierda y 5 de mi mano derecha. Como tu ves el simétrico, ¡observarás 54!
- 9x7=63 Bajando el dedo índice de la mano izquierda veremos 3 dedos y luego 6. ¡El 63!
- 9x8=72 Ahora le toca el turno al dedo corazón de mi mano izquierda y así, ¡obtenemos el 72!
- 9x9=81 Es el anular de la mano izquierda el que se encoge y así nos quedan 8 dedos a tu izquierda y 1 dedo a tu derecha. ¡81!
- 9x10=90 Al bajar el meñique de la mano izquierda sólo vemos 9 dedos... 9 i 0... así que ¡obtendremos el 90!!
¡Gracias a ellos y a todos los demás porque cuando compartes con alguién tus sueños, el amor se multiplica! ¡Multipliquemos!!

18 comentarios:
Molt bona aquesta regla pnemotècnica! En sé algunes amb els dits o amb els nussos, però aquesta en concret no la sabia, i és francament molt maca... La posaré en pràctica!!
Molts records per als teus pares, i per a tu, de part d'algú que també, fa temps, va sentir una fascinació especial davant d'una Transformada de Fourier, i que encara avuí dia s'emociona amb el goig i la fascinació que senten algunes persones davant les petites meravelles que ens ofereix el Cosmos...
Que conserveu aquest goig i aquesta fascinació per sempre!!
J.A.
Hola!
Interessant! El 9 té unes propietats curioses. És molt interessant també la prova del 9 per saber si s'ha dividit correctament. Jo no ho faig perquè les màquines (o la operació inversa) m'estalvien aquesta tasca...però és curiosa.
Suposo que totes les gràcies del 9 són degudes a què utilitzem un sistema decimal...no ho he pensat gaire...algú en té + informació?
Fa temps vaig trobar aquest vídeo que amb el teu escrit he "recuperat":
http://www.youtube.com/watch?v=k-69kQVD_Ws
a on es mostra una manera diferent de multiplicar/sumar de la que ens han ensenyat.
Salut,
Victor
Gràcies Jordi!!
Ei Víctor! Jo tampoc li havia donat massa voltes a això que dius de les propietats del 9... Ja ho investigaré!
Per cert, el vídeo és boníssim!!! Em sembla fascinant... Això sí que no ho havia vist mai!! També vull pensar-hi!
A veure si en ajuda algun matemàtic?!! Jo tinc una ex-alumna que actualment estudia matemàtiques a la UB... A vere, a vere...
Mil gràcies als dos!!!
Muy bonita la entrada.
Por lo emotivo y... por la preciosa transformación de Fourier. Para quien no lo sepa lo que duerme debajo del jpeg y del mp3.
Por si te sirve, aquí va otro truqui con las manos. Lo llaman multiplicación rusa y sirve para multiplicar dos números comprendidos entre 6 y 10.
http://lubrin.org/spip.php?article76
Y para verlo en movimiento.
http://www.youtube.com/watch?v=jVeXT9TkJIE
Javi
En aquest fórum oblidat també hi ha alguna entrada interessant (no sé si certa) sobre les propietats del 9
http://ar.answers.yahoo.com/question/index?qid=20061221033349AAEBcXj
Si mai m'avorreixo, ja sé que d'aquí en puc treure moltes hores...
Torno a escriure perquè he esborrat el comentari anterior ja que m'he fet un embolic i ja no sé ni en quina base escrivia...
Aviam si ara m'aclareixo:
A en Victor, la prova del 9 pel que he pogut veure en uns quants càlculs que he fet sobre la marxa, funciona a altres sistemes (he provat amb l'octal). Així que potser hauria de deixar de dir-se prova del 9 :p
Exemple: 17572:355=42 (octal)
Si sumem en octal 1+7+5+7+2=26;2+6=10; 1+0=1
Ara sumem 3+5+5=15;1+5=6
i 4+2=6
Així 6x6=44 (octal) 4+4=10; 1+0=1
És a dir la prova del 7 també es verifica en base octal :p
A banda, un comentari crític amb el sistema educatiu. Molta de la gent que de gran diu "uff, les matemàtiques... és que no puc..." acaba anant a les taules de multiplicar com arrel dels seus problemes. I és que a molts llocs les fan memoritzar i a l'edat que tenim quan les aprenem molts tenen problemes per memoritzar una cosa que no poden identificar amb res. Potser seria molt millor intentar explicar el concepte o deixar-ho per més endavant quan ja estiguessim preparats per entendre el mòn abstracte de les matemàtiques.
També vull unir-me al club d'admiradors de la transformada de Fourier. Una de les coses més espectaculars és que apareix des de la Teoria de cordes fins els algoritmes de reconstrucció d'un tomògraf. I una cosa que apareix fractamel a tots els àmbits de la física ha de tenir alguna cosa a veure amb l'estructura de la realitat, oi?
Salut!
Oh! Un post de Matemàtiques! Aquesta transformada de Fourier em sona, diria que sí que he fet quelcom semblant a Probabilitat... El nou és un nomrbe ben curiós, fa poc em van enviar un correu que tenia a veure amb aquest nombre (el correu en sí és una xorrada) però és curiós. Ja te'l enviaré.
Cris
Bé, i ara torno a escriure per reescriure el que abans he esborrat perquè m'havia fet un embolic.
Això de multiplicar amb els dits es pot fer servir per fer productes en qualsevol base.
Si volem multiplicar en octal, mantenim nomes 8 dits inicials. Si volem multiplicar en base 5, fem servir només una mà.
Sí, pot ser tinc molt de temps lliure... algú vol venir a fer una birra?
Molt curiós!
Explorant pel Youtube es troba la teva explicació vista des del cantó del qui ho fa.
http://www.youtube.com/watch?v=gKA4z3Ssmso
Hola a todos!
Primero, quiero daros las gracias a todos por ir dejando vuestros comentarios. Gracias!!
He estado mirando los escritos, foros y vídeos que nos recomendabais... Y hay de bien curiosos!!
La manera de multiplicar a la Rusa... no está nada mal Javi... Mil gracias!!
Y como dice Ramon, si en lugar de experimentarlo desde el punto de vista de un/a observador/a (como fue mi caso, en casa de mis padres), lo queréis practicar vosotros, lo podéis hacer siguiendo las instrucciones de youtube.
Por cierto dt, me han gustado mucho tus intervenciones... Creo que la vida bella de Canarias te ayuda a tener la mente muy depejada... Un crack! Gracias!!
Pues eso... como dice Víctor... que quien se aburre es porque quiere... ya que simplemente con los números y sus operaciones podríamos llegar a pasarnos una eternidad jugando y reflexionando...
A pensarlo!!!
Mua!!!
ila
Ai, les taules de multiplicar!
Jo sempre em feia un embolic amb la del 8, la del 9 com que era simètrica no era tan complicada, però al del 8…
I crec que en dt té raó amb la crítica que fa: jo vaig memoritzar les taules de multiplicar i realment les matemàtiques em costaven molt perquè no les comprenia i no es prenien gaires molèsties en ajudar-nos a entendre, sinó a resoldre…
En fi, salutacions!
Hola Esther!
Sí, jo també penso que didàcticament les hauríem de revisar!
La reflexió aquesta d'explicar el concepte i de no jugar tant amb la memòria o fer-ho per partida doble o més endavant, no em sembla pas dolenta...
És una pena que hi hagi tanta gent que no pugui hgaudir de les matemàtiques per una mala pedagodia...
Mates i salut!
ila
Crec que el problema sovint està en basar les mates en les taules de multiplicar perquè a la majoria de gent li agraden les mates (encara que no ho sàpiguen) però no volen memoritzar xifres ni operacions. Històricament la gràcia de les mates ha estat quantificar, i han estat molt útils! però per començar he pensat moltes vegades que és millor tractar-les d'una forma qualitativa (proporcionalitats, variacions d'una certa variable, gràfiques sense valors, etc.), sense números! Així, el fet de sumar o multiplicar esdevindrà una necessitat per tal de poder avançar. A mi de petit m'agradava escoltar contes però quan vaig haver de començar a analitzar les frases i vigilar l'ortografia, va perdre part del seu encant. I sí, m'apunto a fer unes birres Toni!
Tot i que no ho referencio, em penso que la didàctica de les matemàtiques es centra molt en aquests aspectes, però no crec que aquests canvis es manifestin en futur proper...
Salut,
Victor
Per cert, veient tantes formes que hi ha de sumar, multiplicar, etc. veig que la taula de multiplicar al disc dur acaba siguent el millor (almenys per a mi) i que cadascú utilitzi la regla mnemotècnica que més li convingui. Hi ha cada mètode més extrany amb tantes condicions i excepcions....
Em recorda tot això a la gent que per no memoritzar fòrmules, s'ho apuntava a la calculadora gràfica i que per saber-ho, t'havies de llegir un "totxo" d'instruccions i tardaves casi més temps i "utilitzaves" més disc dur...
Victor
Has puesto 2 veces 9x8 i 9x9 no son 81.
Ricardo Caballero
Gracias Richard!
Ya está corregido... Un despiste tipográfico...
Espero que aún así te sigas pasando por la mandarina.
¡Hasta pronto!
ila
Hola, muy bueno este ejemplo. Esta semana santa tu padre nos la explicó en casa, pero al que más falta le hacía (a Mario, el pequeño de mi hermano que está con las tablas de multiplicar) parece ser que no le hizo mucho entusiasmo.
Publicar un comentario