Cócteles de ciencia, mates, misterio, crimen y algunas especias más

Esta tarde estaba con un compañero mirando unas preciosas fotografías donde algunas gotas de agua impactaban de vuelta a su fluido. En ese instante, mis propias palabras me han llevado a darme cuenta de que mi pasión son los combinados. No, no penséis que hoy quiero hablar de etanol, propanol o cualquier otro tipo de alcohol, no. Mis cócteles preferidos son los que mezclan ciencia o matemáticas con cualquier otra disciplina, manera de mirar al mundo o forma de sentir-se. Me gusta ver como en la caída de una gota se mezclan belleza, óptica, gravedad y dos componentes químicos: el hidrógeno y el oxígeno. Me emociona pensar que hay ciencia en cada esquina. Y quiero proponer la fusión más nuclear que las leyes de la física me permitan. Si el Flamenco puede fundirse con el Jazz, las matemáticas pueden mezclarse con los asesinatos y la física con la poesía.

Si a alguien le apetece poner en una misma coctelera: asesinatos, misterio, matemáticas y literatura, recomiendo la lectura, casi enfermiza, de la segunda parte de "Los hombres que no amaban a las mujeres". Es decir, "La chica que soñaba con una cerilla y un bidón de gasolina" de Stieg Larsson. Este libro me sorprendió con frases como la que sigue:

"La raíz de una ecuación es un número que introducido en un lugar de la incógnita hace de la ecuación una identidad. Se dice que la raíz satisface la ecuación. Para resolver una ecuación uno debe encontrar todas las raíces. Una ecuación que es satisfecha por todos los valores imaginables de las incógnitas se conoce como identidad.
(a + b)² = a² + 2ab + b² "

Y no sabemos si son palabras de un libro de texto o de una novela... Y es que la vida también tiene una incógnita o dos o tres o media docena. Una x, una y, una z, una n, una t o una combinación de todas ellas que resuelven el misterio... Cuando quedamos con un amigo, establecemos un tiempo y una posición determinada para que ambos cuerpos puedan tener un punto en común de entre todos los puntos de sus caóticos recorridos. ¡Cuantos trenes se encuentran entre A y B en los libros de texto! ¡Y cuantos amigos se encuentran para ir al cine en las calles de nuestras ciudades! Es exactamente lo mismo... (O una aproximación de lo mismo).

Y es que con este post, intento desagraviar a la ciencia y a las matemáticas de todos los instantes t en que estas son tratadas con desprecio. Rechazo todos esos comentarios sobre que la ciencia o las matemáticas son aburridas y no interesan al ciudadano. Me quejo de todos esos anuncios que vimos de pequeños, los que ahora ya llegamos a los 30, donde decían:

- ¿Las mates? ¡No, esas no entran ni frías, ni calientes!

Porque frías, calientes, con misterio, a palo seco, con ron, con letras griegas, en novelas, en el día a día, en el cine y en la vida, la ciencia y las matemáticas son la esencia y la chispa que nos mueve. No hay nada más curioso que un niño o una niña. Y nada más fascinante que un periodista y reportero de guerra sueco que describe como Lisbeth Salander, una de las protagonistas de sus novelas, de repente, se detiene en seco y...

"En el margen de su ejemplar de Arithmetica, Pierre de Fermat había garabateado las palabras: "Tengo una prueba verdaderamente maravillosa para esta afirmación, pero el margen es demasiado estrecho para contenerla".
El cuadrado se había convertido en un cubo ( cuando n = 3) y los matemáticos habían dedicado siglos a dar respuesta al enigma de Fermat. Para llegar a resolverlo, en la década de los noventa, Andrew Wiles hubo de luchar durante diez años con el programa informático más avanzado del mundo.
Y de pronto, Lisbeth (nuestra protagonista) lo comprendió. La respuesta fue de una sencillez que la desarmó por completo. Un juego de cifras que se alineaban en serie, y de súbito, se colocaron en su sitio formando una fórmula que más bien debía verse como un jeroglífico. (...)"

Eso es lo que necesitamos, más mestizaje, más Lisbeth Salanders resolviendo enigmas de Fermat justo antes de encontrarse con unos asesinos. (Que por cierto, para los que guste el tema de Fermat (y para los que no) también recomiendo la película "La habitación de Fermat"), más Bart Simpsons comprobando el Efecto de Coriolis, más entendimiento a la vida y más realidad al misterio que nos rodea...

Y con esto... ¡Tan sólo desearos suerte, en vuestros cálculos matemáticos y en vuestras incógnitas vivenciales!! ¡¡¡A encontrar las Xs!!!

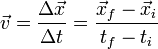
Azul como uma laranja o verde como una mandarina

Hace unas semanas fui a ver un espectáculo de mi profesora de danza, Cecilia Colacrai y de Joao Costa: "Azul como uma laranja". Intentando documentar fotográficamente este post, encontré el blog de la pieza "Azul como uma laranja" y en él encontré algunas fotos de la pieza hechas por Yoana. He elegido una de ellas porque quería que pudierais percibir un instante de la escena, pero os animo a todos a seguir viendo las demás instantáneas que encontraréis en dicho blog.

Tal vez os sorprenda que hoy quiera hablar de danza y espectáculos... ¿Acaso cambio la Mandarina de Newton por la Mandarina de las zapatillas rojas? Y aunque esta Mandarina proviene de bailarina, no es esa la respuesta. Hoy quiero hablar de danza y de Cecilia porque el movimiento, el espacio y el tiempo son los protagonistas de cualquier baile. Son tan artísticos, como Newtonianos, o incluso Einsteinianos.

¿Os habéis dado cuenta de las palabras? Es quizás eso, tan sólo una combinatoria de sonidos y grafías, pero que nos llevan a las variables involucradas en las ecuaciones de movimiento, o ecuaciones de Newton. Espacio, del latín spatium, lugar en el que se ubican los objetos o distancia recorrida por un móvil en un cierto tiempo. Tiempo, magnitud física que mide la duración o separación de acontecimientos sujetos a cambio. La velocidad es la es la magnitud física que expresa la variación de la posición o del espacio, en función del tiempo:

¡La aceleración es la variación de la velocidad en función del tiempo!

Y con ello, ya tenemos todos los ingredientes para poder componer el espacio. Esta es una de las expresiones que más oídas en las clases de Cecilia... "¡¡Compongamos el espacio!!" Y es que la Física, la ciencia, no está exenta ni de belleza, ni de sutileza... ni se guarda en los libros de texto. La Física está en cada rincón del planeta, en cada acción de la vida y en cada giro de una naranja. Ciencia es todo y no es nada... es tan sólo una manera de mirar al mundo y un intento de explicar aquello que hemos visto.

Cecilia nos recuerda que pensemos en los millones de direcciones que nos atraviesan, nos recuerda que los brazos tienen una intención... ¿Sabéis de qué nos habla? ¡De vectores! Cecilia hace cálculo vectorial cada vez que se ata la coleta y se mueve grácilmente por la sala, Cecilia hace cálculo vectorial cada vez que camina y compra una naranja. Un vector, no es nada más que una magnitud física con una longitud (una medida, o el número de pasos que camina), una dirección (una recta por la que se traslada) y un sentido (si sube o baja la calle, si camina hacia la derecha o hacia la izquierda, hacia donde mira su nariz) definidos.

Por no hablar del momento de inercia o inercia rotacional. El momento de inercia es una magnitud escalar, expresada con un sólo número (no como los vectores que necesitan de más información) que refleja la distribución de masas de un cuerpo o de un sistema de partículas en rotación, respecto al eje de giro. El momento de inercia sólo depende de la geometría o forma del cuerpo y de la posición del eje de giro. Una bailarina tiene más momento de inercia si extiendo los brazos a los lados y por eso girará más lentamente. Si, en cambio, contrae los brazos o los sube hacia arriba, consigue que su masa esté más cerca de su centro y por tanto, del centro de rotación, y con ello disminuye el momento de inercia, la resistencia al giro y aumenta su velocidad de rotación.

Nos salió un nuevo término: el centro... Cecilia seguiría insistiendo... "¡No os olvidéis de vuestro centro!". Y no es para menos, y es que nuestro centro de masas se comporta como si toda la masa de nuestro cuerpo estuviera allí colocada. ¿Recordáis los problemas de física de la escuela? Todos trataban sobre partículas puntuales... ¿Y alguien ha visto un punto correr, bailar o comer naranjas? ¡No! Dichos puntos caminantes, bailarines y comedores de naranjas no eran otra cosas que aproximaciones. La Física vive del arte de aproximar... Y de momento no le va tan mal. La mayoría de las veces, el error que cometemos considerando que un humano es un cilindro es tan pequeño, que no vale la pena enfrascarse en un millón de cálculos y complicaciones para incluir todos los detalles, si al final, acabamos consiguiendo, siete días más tarde, un resultado muy cercano al aproximado.

¿Lo veis? La danza es física y es química... (otro día podemos hablar de las reacciones que bailar produce en el cuerpo), y es anatomía y es biología y es todo y no es nada... porque el Universo no tiene etiquetas y porque lo único que cambia es el ojo que lo mira.

"Nombramos las cosas en un intento de re-inventar el mundo a partir de sus nombres. Como si cada cosa existiera a través de su definición. Toda descripción es una sugestión en potencia. El lenguaje revela formas a través de límites, recortes que clasifican y definen las materias. Las im-posibilidades del lenguaje nos invitan a reflexionar sobre otras existencias. Así, nos lanzamos a componer una trayectoria para cada cosa. Un antes y un después, un contexto donde el objeto en cuestión podría habitar, existir. A partir del punto mínimo construimos sus probabilidades. Punto por punto. Y de probable en probable alcanzamos posibles, equilibrándonos entre la ficción y en lo que insistimos en llamar realidad."

(Son las palabras de la ficha técnica del espectáculo...)

¡Litografías con historias!

¿Cuándo fue la última vez que me senté delante de mi querido MacBook a redactar algunas líneas sobre ciencia, vida y pensamientos? ¡Uf! Ya casi ni me acuerdo...

Siento estas tres semanas de silencio, pero en unos días mi vida ha participado de varios cambios sísmicos. Con tanto ajetreo, me había alejado provisionalmente de estos momentos de reflexión. Sí, podéis decirme: "¿Cambios? ¿Te asustas de algo tan simple y cotidiano como el cambio? Si el Universo es tan sólo eso, una sucesión de estados, un conjunto de cambios... Nada es inmutable. ¡Ni tan siquiera los cielos!". ¡Y cuanta razón tendrías! Pero yo os respondería: "Sé que he hecho un pequeño paso para la humanidad, pero un gran paso personal"

¿A qué vienen tanto misterio? Dejaré que os lo desvelen las piedras... ¡¡Os susurraré a gritos mis novedades!! Desde hace tres semanas soy la nueva Responsable de Comunicación del Instituto Catalán de Paleontología Miquel Crusafont (ICP). Durante estos días me he dejado impresionar por dientes minúsculos de pequeños roedores, grandes mandíbulas donde cada diente era como un puño humano y el esmalte aún brillaba, historias de musarañas, rastros de dinosaurios y cortes histológicos de huesos petrificados. ¡Increíble!

La Paleontología (del griego palaios= antiguo, onto= ser, logos= ciencia) es la ciencia que estudia e interpreta el pasado de la vida sobre la Tierra a través de los fósiles, restos de seres que vivieron en un pasado lejano, petrificados, o de su actividad. Se encuadra dentro de las Ciencias Naturales y comparte fundamentos y métodos con la Geología y la Biología.

Para mi, todas las piezas que me han ido mostrando durante estos días no dejan de ser obras de arte del tiempo... Litografías. Impresiones. Dibujos en la piedra realizados con moldes de un pasado. Seres que habitaron el mismo planeta que tu y yo compartimos hoy... Murieron, se compactaron y se petrificaron. Bellezas naturales que superan la imaginación de artistas y cuenta cuentos. Historias atrapadas entre papeles rocosos. Evoluciones. Y como siempre... ¡Cambios!.

Sé que en esta nueva etapa, tendré que hincar los codos y volver a la escuela de los libros y la as lecciones de los investigadores y profesionales del ICP, pero me lo tomo con muchísima ilusión e interés. No haré este camino sola, el personal del Instituto me acompaña, pero además, conociéndome, vosotros también podréis ir siguiendo algunos de mis excursiones al pasado. Es curioso, tantos años dedicada a la Física, estudiando conos de tiempo y aceptando la imposibilidad de los viajes hacia pasados y futuros.... y ahora me encuentro inmersa en la ciencia de lo remoto conquistando el futuro!

Deseadme buena suerte y prometo seguir informando...

Recuperando las tablas...

¿Recordáis aquellos años en los que las clases de matemáticas se transformaban en un sinfín de actividades para aprenderse las tablas de multiplicar? ¡Qué momentos!

No sé... tal vez, es tan sólo una impresión personal, pero creo que a la edad de siete o ocho años, una de las cosas más importantes que aprendes son las tablas de multiplicar. Porque esos números alineados y agrupados que simbolizan la compresión de la suma son mucho más que números. Tienen más representaciones y simbolismos. Uno de ellos, es el de que ya eres "mayor". La gente te pregunta ¿Ya sabes multiplicar? Y todo orgulloso o orgullosa respondes, sí, me sé hasta la tabla del... y añades el 6, el 7 o el número de la tabla que estés estudiando en ese momento. Esa sensación de estar descubriendo el mundo y de entrar en los conceptos difíciles, vuelve cuando aprendes a dividir por dos cifras o cuando despejas la primera incógnita de tus ecuaciones. Pero poco a poco, parece que se va difuminando y va perdiendo intensidad...

No negaré, que la Transformada de Fourier estudiada durante mis años universitarios (una aplicación que hace corresponder a una función f con valores complejos y definida en la recta, otra función g definida de la manera siguiente:

)

también me produjo una alegría comparable a la de saber multipilicar... Curiosamente, esta operación matemática está basada en una integral... que no deja de ser la suma de trocitos muy pequeñitos... ¿Tendrán las sumas comprimidas algo especial? ¡Quien lo sabe!

Pero volvamos a las multiplicaciones... ¡A esa primera vez, y a esa tabla del 9! Este fin de semana fui a comer a casa de mis padres, en medio del campo... Y fue entre las montañas, que mi padre me preguntó:

-Irene, a tí te gusta explicar anécdotas de ciencia, matemáticas, tecnología... ¿cómo explicarías tú la tabla del nueve?-

Yo acepté el reto y le comenté... pues diria que multiplicar por nueve es sumar nueve veces el número elegido...

A lo que él me respondió:

-Sí, teoricamente me parece bien... pero ¿Quieres sorprenderte con una regla pnemotécnica que encontré por Internet?!! Mira, extiendo mis dos manos y vamos a contar dedos:

• 9x1=9 Si encojo el dede meñique de mi mano derecha y cuentas los dedos que todavía tengo estirados verás que son exactamente 9
• 9x2=18 Si encojo el dedo anular de mi mano derecha (el siguiente al meñique), verás que me queda un dedo a tu izquierda y ocho a tu derecha, lo que dibuja ¡un 18!
• 9x3=27 Esta vez encogeré el dedo anular y me quedarán el dede meñique y el anular de la mano derecha a tu izquierda y siete dedos más a tu derecha. ¡27!
• 9x4=36 Bajaré el índice de mi mano derecha y obtendré 3 dedos a tu izquierda y 6 a tu derecha. ¡36!
• 9x5=45 Bajaré el pulgar y veremos 4 y5. ¡45!
• 9x6=54 Esta vez, encogeré el pulgar de la mano izquierda y así veremos 4 dedos de mi mano izquierda y 5 de mi mano derecha. Como tu ves el simétrico, ¡observarás 54!
• 9x7=63 Bajando el dedo índice de la mano izquierda veremos 3 dedos y luego 6. ¡El 63!
• 9x8=72 Ahora le toca el turno al dedo corazón de mi mano izquierda y así, ¡obtenemos el 72!
• 9x9=81 Es el anular de la mano izquierda el que se encoge y así nos quedan 8 dedos a tu izquierda y 1 dedo a tu derecha. ¡81!
• 9x10=90 Al bajar el meñique de la mano izquierda sólo vemos 9 dedos... 9 i 0... así que ¡obtendremos el 90!!

¡¡No os parece estupendo!! Agradezco a mis padres la paciencia que tuvieron en su día, ayudándome a ver las tablas de multiplicar como un juego divertido, enseñándome a leer y a querer leer todo lo que estuviera escrito, a ser curiosa y por ello, a ser científica. También les doy las gracias hoy por seguirme apoyando, por seguir sorprendiéndome con algo tan simple como son las tablas de multiplicar y por semana tras semana ir leyendo La Mandarina de Newton!!

¡Gracias a ellos y a todos los demás porque cuando compartes con alguién tus sueños, el amor se multiplica! ¡Multipliquemos!!

TecnoLab, una nueva propuesta para pensar, tocar, buscar y crear

Hace unas semanas inicié un nuevo proyecto en Citilab Cornellá llamado TecnoLab. Es un curso de talleres de tecnología para niños y niñas de 7 a 9 años. Durante 8 sesiones analizaremos conceptos como las TIC, los píxels, los programas i virus informáticos, los códigos o Internet, entre otros. Para hacerlo utilizaremos diferentes estrategias como la documentación, la experimentación o la creación. Combinaremos actividades de plástica, mecánicas o de experiencia real.

El primer día, por ejemplo, entendimos qué eran las TIC gracias al juego del teléfono. También visualizamos los píxels coloreando el mismo dibujo con diferentes estrategias: colores de madera, pegatinas cuadradas de un sólo color muy pequeñas, pegatinas mono color cuadradas más grandes. Sí, comprobamos que con los píxels mayores perdíamos definición. Finalmente, un programa de tratamiento de imágenes nos ayudó a verlo en vivo y en directo.

El segundo día exploramos qué son los programas y los virus informáticos. Y gracias a un juego de sobres y tarjetas jugamos a ser programadores y máquinas programadas. ¡Hubo un chico travieso que quería destrozarnos a todos con sus órdenes malignas!! Finalmente, acabamos programando en Scratch!

También me gustaría promover el ser capaz de exponer aquello aprendido a los demás y comunicar ideas en público. Soy de la opinión de que en este país, muchas veces nos olvidamos de este punto... Y a mi, persona dicharachera y farandulera de nacimiento, me parece un error. Creo que deberíamos mezclar todos los sentidos cada vez que nos proponemos enseñar o aprender algo. Es importante que en matemáticas se dibujen los hexágonos y se escuchen los pentagramas... Es imprescindible que en la clase de química se huela el ácido sulfhídrico, se toque una base o se escuche la explosión del hidrógeno...

He de decir que cada día que pasa, la tecnología y en concreto la informática, me cala un poquito más hondo... pero igual que entro salgo (como un chiste de informáticos) y desde fuera percibo que algunos se quedan delante de la pantalla observando combinaciones de rojo, azul y verde... ¡¡Salgamos!! Mostremos la tecnología y la vida, en todas sus direcciones. Con un poco de ingenio, paciencia, esfuerzo y confianza en lo nuevo podremos hacerlo... Conseguiremos hablar de ratones informáticos con un destornillador, un papel y un bolígrafo e Internet.

Pienso que TecnoLab puede ser un reto. Espero poder conquistarlo sin problema... Y los comentarios son siempre bienvenidos... Eso sí, cuando Eric, un niño de 9 años que ya ha publicado su propio blog (http://petitreporter.blogspot.com/) te mira a los ojos y te comenta: -¡Ahora sí que me has sorprendido! ... Claro, ¡hay que programarlo todo! ¡Sin un programa previo la impresora no sabría escribir lo que yo imprimo!- O Lucas llega al final de la clase de una hora diciendo: -¿Ya se ha acabado? ¡Pero si sólo pasaron 10 minutos!-. Piensas que seguro que puedes mejorarlo... pero que al menos, parece que acertaste en un trozo del camino, aunque sólo fuera en un rango impreciso de este!! Ahora, entre todos iremos mejorando la definición y disminuyendo el tamaño de los píxels!!

Miss Mandarin viaja a una velocidad de...

Hace un tiempo yo trabajaba como profesora de secundaria y bachillerato de matemáticas, física, tecnología, y otras asignaturas... Recuerdo que disfrutaba preparando los exámenes y no porque los hiciera excesivamente difíciles, sino porque me gustaba poner preguntas personalizadas. Creo, que incluso podría decir que alguno de mis alumnos también esperaba impaciente para leer los nuevos enunciados. Solía utilizar los nombres e los chicos y chicas de clase para nombrar a los personajes de cada problema y en la medida de lo posible los problemas se relacionaban con sus aficiones. Así, por ejemplo, si Joan quería ser piloto de aviones, en un ejercicio de cinemática saldría un avión Boeing 747, por ejemplo, pilotado por Joan. si a Felipe, Óscar o Albert les gustaba la música, ellos encontraban un disco que giraba a tantas revoluciones por minuto (r.p.m.) en el trastero de la abuela. Y así sucesivamente...

¿Por qué os lo cuento? Primero porque creo que es una buena estrategia para los exámenes... Laboriosa porque cada vez debes pensar en el grupo al que enseñas, pero muy constructiva. Y segundo porque hoy me siento como si hubiera pasado un examen de cinemática en vivo y en directo. Miss Mandarin, yo misma, ¡he vuelto a conducir! ¡¡Me he puesto en movimiento!!

El movimiento se define como el cambio de la posición de un cuerpo a lo largo del tiempo respecto un sistema de referencias. ¡Este sistema es imprescindible! Si no lo tengo, no puedo percibir el movimiento... De hecho, aunque no llevara coches, estos últimos años, yo me movía. Me movía caminando, me movía en bicicleta, me movía en autobús... ¿Y sabéis cómo más me movía? ¡¡Dando vueltas alrededor del Sol!! Pero jamás lo noté... ni yo, no vosotros porque todo nuestro sistema de referencias, la Tierra también daba vueltas alrededor del Sol...

Volviendo a la Tierra, con nuestro sistema de referencias fijado y centrándonos en el movimiento, diré que el estudio de este se puede realizar a través de la cinemática o través de la dinámica. La cinemática estudia las ecuaciones del movimiento teniendo en cuenta la posición, la velocidad, la aceleración y el tiempo. La dinámica se pregunta el por qué de el movimiento y analiza sus causas, las fuerzas.

Si construyera un problema cinemático con la experiencia de Miss Mandarin podría escribir...

"Miss Mandarin viaja en un coche a 50km/h. Ha estado 40minutos al volante. ¿Cuántos metros ha recorrido?"

Yo les recomiendo que primero pasen todas las variables a las mismas unidades...
v= 50km/h t= 40min.(1h/60min)= 0'66h
x= v·t x= 33'333km=33.333m

¡Hicimos el problema de cinemática de 3º o 4º de ESO! Y de la dinámica... ¿qué decir? Que fue Newton quien postulo las tres leyes más importantes!!

1. Primera Ley de Newton o Ley de Inercia: Todo cuerpo mantiene su estado de reposo o movimiento uniforme y rectilíneo en ausencia de fuerzas que le obliguen a cambiar su estado. ¡Por eso sabemos que siempre que un cuerpo gira, existe una fuerza!
   
2. Segunda Ley de Newton o Ley de Fuerza: El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime. Esta ley se suele expresar matemáticamente como F=dp/dt= d(m·v)/dt= (dm/dt)·v + m(dv/dt)= 0+ m·a. Es decir la fuerza es el cambio de la cantidad de movimiento (masa por velocidad) en función del tiempo y esto acaba expresándose en la mayoría de casos como la fuerza es igual a la masa por la aceleración.
3. Tercera Ley de Newton o Ley de Acción y Reacción: Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en direcciones opuestas. ¡Gracias a esta ley los humanos caminamos hacia delante o los cohetes salen volando!

Miss Mandarin ha viajado a 50km/h por las calles de Barcelona... ¡Esperamos que eso no sea ningún problema, ni cinemático, ni dinámico! ¡Y que siga circulando!!

La Mandarina va creciendo... ¿Llegará a ser naranja?

Faltan tres días para que La Mandarina de Newton cumpla seis meses de existencia. Durante este tiempo, vosotros habéis ido colaborando conmigo para ir consiguiendo poco a poco generar debates y conversaciones científicas, tecnológicas y humanas. ¡Muchas gracias!

En este post de cumplemeses, quiero enseñaros la cara de La Mandarina de Newton. Esta foto, realizada por Arnór Skuli de Raykjavik, se ha convertido en mi logo mandarinero. También me gustaría hablaros de la genealogía mandarinera:

La Mandarina es el fruto del mandarino. Pertenece al grupo de frutos llamados hesperidios y su pulpa está formada por un considerable número de gajos llenos de jugo; el cual contiene mucha vitamina C, flavonoides y aceites esenciales. Es el cítrico más parecido a la naranja, aunque de menor tamaño, sabor más aromático y con mayor facilidad para quitar su piel. Por eso se considera una de las frutas más apreciadas. La mandarina proviene de las zonas tropicales de Asia; y se cree, que su nombre se debe al color de los trajes que utilizaban los mandarines, gobernantes de la antigua China. En algunos países latino americanos se le llama naranja china.

Yo mi vinculé a las mandarinas gracias a Bruno, el protagonista de un libro de lectura que cayó en mis manos cuando yo tenía, tan sólo, 6 años. Bruno tenía que escribir una redacción sobre un miembro de su familia, y eligió a su hermana. Bruno contaba que su hermana quería ser mandarina y su profesora extrañada le decía que su hermana no podría ser la fruta del mandarino. Pobre Bruno... pobre hermana... Ella lo que quería ser... era... ¡bailarina! Yo, también quise ser bailarina durante algún tiempo... hasta que de repente, una día, estudiando física a altas horas de la tarde... caí en la cuenta de que en realidad no sería bailarina... Yo sería mandarina.

Caí como caen las mandarinas, y como podrían haber caído las manzanas. ¿Manzanas Newtonianas? Sí, las mismas... Esas manzanas que popularizaron al físico, matemático y astrónomo inglés de finales del siglo XVII, principios del siglo XVIII, Newton.

Newton es considerado uno de los científicos más brillantes de la historia. La Ley de la gravitación universal, fue seguramente su aportación más importante y conocida. Según esta ley, la atracción de dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. La Ley de la gravitación es la responsable de que la Tierra orbite alrededor del Sol, que la Luna nos acompañe dando vueltas alrededor de la Tierra, que los objetos se caigan al suelo o de que podamos llevar pendientes. Su obra más destacada es Principios matemáticos de la filosofía natural. En ella, Newton recoge las leyes que constituyen la base de la dinámica, o del estudio de fuerzas. Curiosamente, Newton nació el mismo año en que murió Galileo, el padre de la ciencia moderna y de quién ya he hablado brevemente en un post anterior. Algunos consideran este detalle como un símbolo de la continuidad en el avance de la historia de la Física.

Con esta curiosidad me despido por hoy. Eso sí, deseando que las mandarinas sigan avanzando aunque sin llegar a ser naranjas o pomelos, que la Física siga estudiando, las caídas, los cuerpos, las cuerdas y el Universo, que sigamos divulgando y que vosotros continuéis apreciándolo. Un saludo a todos y gracias por estar al otro lado.